PHYS 4430

Gaussian Beams - Week 4

Contents

1 Goals

In week one, we measured the profile of the laser and found it to be Gaussian to a good approximation. However, we don’t have any model for how the profile changes as the beam propagates and we will work to improve our model. Also, we will apply automation to more rapidly take data. The full set of learning goals includes:

  1. Automated data acquisition.
    • LabVIEW
    • USB DAQ (NI USB-6009)
  2. Fitting and analysis of data in Mathematica
  3. Using a predictive model of Gaussian laser beams
    • Contrast Gaussian beams with geometric optics
  4. Measure profiles of a Gaussian beam, and extract the Gaussian beam parameters
  5. Effect of a lens on Gaussian beams.
    • Is it still Gaussian?
    • Does the thin lens equation apply to Gaussian beams?
    • What limits the minimum achievable spot size?

2 Prelab

Light is a propagating oscillation of the electromagnetic field. The general principles which govern electromagnetic waves are Maxwell’s equations. From these general relations, a vector wave equation can be derived.

\[ \nabla^2\vec{E}=\mu_0\epsilon_0 \frac{\partial^2\vec{E}}{\partial t^2}\text{.}\](1)

One of the simplest solutions is that of a plane wave propagating in the \(\hat{z}\) direction:

\[\vec{E}(x,y,z,t)=E_x\hat{x}cos(kz-\omega t+\phi_x)+E_y\hat{y}cos(kz-\omega t+\phi_y)\text{.}\quad\quad\](2)

But as the measurements from the first week showed, our laser beams are commonly well approximated by a beam shape with a Gaussian intensity profile. Apparently, since these Gaussian profile beams exist, they must be solutions of the wave equation. The next section will discuss how we derive the Gaussian beam electric field, and give a few key results.

2.1 Paraxial wave equation

One important thing to note about the beam output from most lasers is that the width of the beam changes very slowly compared to the wavelength of light. Assume a complex solution, where the beam is propagating in the \(\hat{z}\)-direction, with the electric field polarization in the \(\hat{x}\)-direction:

\[\vec{E}(x,y,z,t)=\hat{x}A(x,y,z)e^{kz-\omega t}\text{.}\](3)

The basic idea is that the spatial pattern of the beam, described by the function \(A(x,y,z)\), does not change much over a wavelength. In the case of the He-Ne laser output, the function \(A(x,y,z)\) is a Gaussian profile that changes its width as a function of \(z\). If we substitute the trial solution in Equation 3 into the wave equation in Equation 1 we get

\[\hat{x} \left[ \left(\frac{\partial^2A}{\partial x^2} +\frac{\partial^2A}{\partial y^2} +\frac{\partial^2A}{\partial z^2} \right) +2ik\frac{\partial A}{\partial z} - k^2A \right]e^{i(kz-\omega t)}=\hat{x}\mu_0\epsilon_oA(-\omega^2)e^{i(kz-\omega t)}\text{.}\quad\quad\](4)

This can be simplified recognizing that \(k^2=\omega^2/c^2=\mu_0\epsilon_0\omega^2\), where the speed of light is related to the permeability and permittivity of free space by \(c=(\mu_0\epsilon_0)^{-1/2}\). Also, the \(\hat{x}e^{i(kz-\omega t)}\) term is common to both sides and can be dropped, which results in

\[\left(\frac{\partial^2A}{\partial x^2} +\frac{\partial^2A}{\partial y^2} +\frac{\partial^2A}{\partial z^2} \right) +2ik\frac{\partial A}{\partial z}=0\text{.}\quad\quad\](5)

So far, we have made no approximation to the solution or the wave equation, but now we apply the assumption that \(\partial{A}(x,y,z)/\partial{z}\) changes slowly over a wavelength \(\lambda = 2\pi /k\), so we neglect the term

\[\left| \frac{\partial^2A}{\partial z^2} \right| \ll \left|2k\frac{\partial A}{\partial z}\right|\text{.}\](6)

Finally, we get the paraxial wave equation,

\[\frac{\partial^2A}{\partial x^2} +\frac{\partial^2A}{\partial y^2} +\frac{\partial^2A}{\partial z^2}=0\text{.}\](7)

One set of solutions to the paraxial wave equation are Gauss-Hermite beams, which have an intensity profiles like those shown in Figure 1. These are the same solutions as for the quantum simple harmonic oscillator, a topic that could be further explored as a final project.

The simplest of these solutions is the Gaussian beam, which has an electric field given by

\[\vec{E}(x,y,z,t) = \vec{E}_0\frac{w_0}{w(z)}exp\left(-\frac{x^2+y^2}{w^2(z)}\right)exp\left(ik\frac{x^2+y^2}{2R(z)}\right)e^{-i\zeta(z)}e^{i(kz-\omega t)}\text{,}\quad\quad\](8)

where \(\vec{E_0}\) is a time-independent vector (orthogonal to propagation direction \(\hat{z}\)) whose magnitude denotes the amplitude of the laser’s electric field and the direction denotes the direction of polarization. The beam radius \(w(z)\)is given by

\[w(z)=w_0\sqrt{1+\left(\frac{\lambda z}{\pi w_0^2}\right)^2}\text{.}\](9)

\(R(z)\),the radius of curvature of the wavefront, is given by

\[R(z)=z\left(1+\left(\frac{\pi w_0^2}{\lambda z}\right)^2\right)\text{,}\](10)

and the Gouy phase is given by

\[\zeta(z)=arctan\frac{\pi w_0^2}{\lambda z}\text{.}\](11)

The remarkable thing about all these equations is that only two parameters need to be specified to give the whole beam profile: the wavelength \(\lambda\) and the beam waist \(w_0\), which is the narrowest point in the beam profile. There is a more general set of Hermite Gaussian modes which are shown in Figure 1. The laser cavity typically produces the (0,0) mode shown in the upper left corner, but an optical cavity can also be used to create these other modes – a topic that can be explored in the final projects.

Figure 1: Intensity distributions for the lowest order Gauss-Hermite solutions to the paraxial wave equation. The axes are in units of the beam width, \(w\).

2.2 Trying out the gaussian beam model

In the first week of the lab, we assumed the intensity profile of the Gaussian beam was given by \(I(x,y)=I_{max}e^{-2(x^2+y^2)/w^2}\). The equation for the electric field of the Gaussian Beam in Equation 8 looks substantially more complicated.

  1. How are the expressions for electric field and intensity related?
  2. Is Equation 8 consistent with the simple expression for intensity \(I(x,y)=I_{max}e^{-2(x^2+y^2)/w^2}\)?

The Gaussian beam equations given in Equations 8 11 assume the beam comes to its narrowest width (called the beam waist, \(w_0\)) at \(z=0\).

  1. How would you rewrite these four equations assuming the beam waist occurs at a different position \(z=z_w\)?
  2. One way to check your answer is to make sure the equations simplify to Equations 8 11 in the special case of \(z_w=0\).
  3. Write a function to fit this data set. Assume the wavelength is \(\lambda=632.8\ nm\).
  4. What is the functional form for your fit function?
  5. What are the different fit parameters and what do they mean?
  6. Is it a linear or nonlinear fit function? Why?
  7. You should get that a beam waist of \(w_0=(93.9\pm0.1)\times10^{-6}\ m\) and occurs at a position \(z_w=0.3396\pm0.0003\ m\).

3 Automation of the Measurement

Before we begin this week’s lab, reflect on your experience from week one (and perhaps refer to your lab notebook entry to help guide your memory).

  1. In week one, how long did the total process of data taking through analysis take to make a measurement of the beam width \(w\)?
  2. In this lab, you may have to take 20-30 beam profiles in order to measure \(w_0\) and \(z_w\). How long would this take with your current method?
  3. What are the most time consuming portions of the process? Which parts of the process would benefit from automation?

In the next step, you will use LabVIEW and your NI USB-6009 data acquisition device to automate the procedure for measuring the width of the laser beam. You can do this with your own laptop or with the laptops in the lab.

In order to set up your measurement automation you will need to create a LabVIEW VI that performs the automated data taking (moving the translation stage, recording the position, recording the voltage from the photodiode, repeat). Instructions can be found in the Appendix 5.

  1. Test and run the automated LabVIEW program and evaluate the result using the same Mathematica analysis from week one.
  2. Before you go on, make sure the automated acquisition and analysis routine gives the same result as the method you used in week one.
  3. How long does your new measurement method take? (2-3 minutes per \(w\) measurement is very good.)

4 The Experiment

The Gaussian beam model of light is useful because it often describes the beam of light created by lasers. This section will test the validity of the model for our He-Ne laser beam. Also, the effect of a lens on a Gaussian beam will be tested, and the Gaussian beam model will be compared with predictions from the simpler ray theory. Lastly, the Gaussian beam theory can be used to describe the minimum possible focus size for a beam and a lens.

4.1 Measuring the beam profile of your He-Ne laser without any lenses

There is a straight-forward reason that a He-Ne laser should produce a Gaussian beam. The laser light builds up between two mirrors, and the electromagnetic mode that best matches the shape of the mirrors is the Gaussian beam.

  1. Considering Equations 8 11, which aspects of the Gaussian beam model can you test? Are there any parts of the model you cannot test?
  2. Measure the beam width \(w\) at various distances from the laser. Consider carefully what distance should be varying. Is it the distance from laser to razor, the distance from razor to photodetector, or the distance from laser to photodetector? How did you decide what positions \(z\) to measure the width at (meter sticks and other measurement tools are available in the lab)?
  3. Fit the data to \(w(z)\), the predicted expression for a Gaussian beam given in Equation 9.
  4. What is the value of the beam waist \(w_0\) (including uncertainty)? Where does the beam waist \(z_w\) occur relative to the laser?

4.2 How does a lens change a Gaussian beam?

Pick a non-compound lens (not the fancy camera lenses) with focal length in the range 100-200 mm and assemble it in a lens mount with a retaining ring (see Figure 2). Recall that it’s very important that you do not handle optical components (lenses, mirrors, polarizers, wave plates, beam splitters, etc.) with your bare hands. The oils on your skin can damage the optics and degrade the light in your experiment. Always handle these components while using latex/nitrile gloves or finger cots.

Design and carry out an experiment to quantitatively answer the questions below. Consider carefully where to put the lens. Your data for this section can be used in the next section.

  1. Insert a lens (after the mirrors) into the beam path to change the divergence/convergence of the beam but keep its propagation direction the same.
  2. When this condition (the beam propagation direction is unchanged) is met, where does the beam intersect the lens? Note: This is the preferred method of adding a lens to an optical set up.
  3. Does the beam retain a Gaussian profile after the lens?
  4. What is the new beam waist \(w_0\) and where does it occur?
  5. What factors affect the beam profile after the lens?
  6. Does the measured \(w(z)\) match the Gaussian beam prediction given in Equation 9?
Figure 2: Mounting assemblies for a mirror (left) and a lens (right).

4.3 Quantitatively modeling the effect of a lens

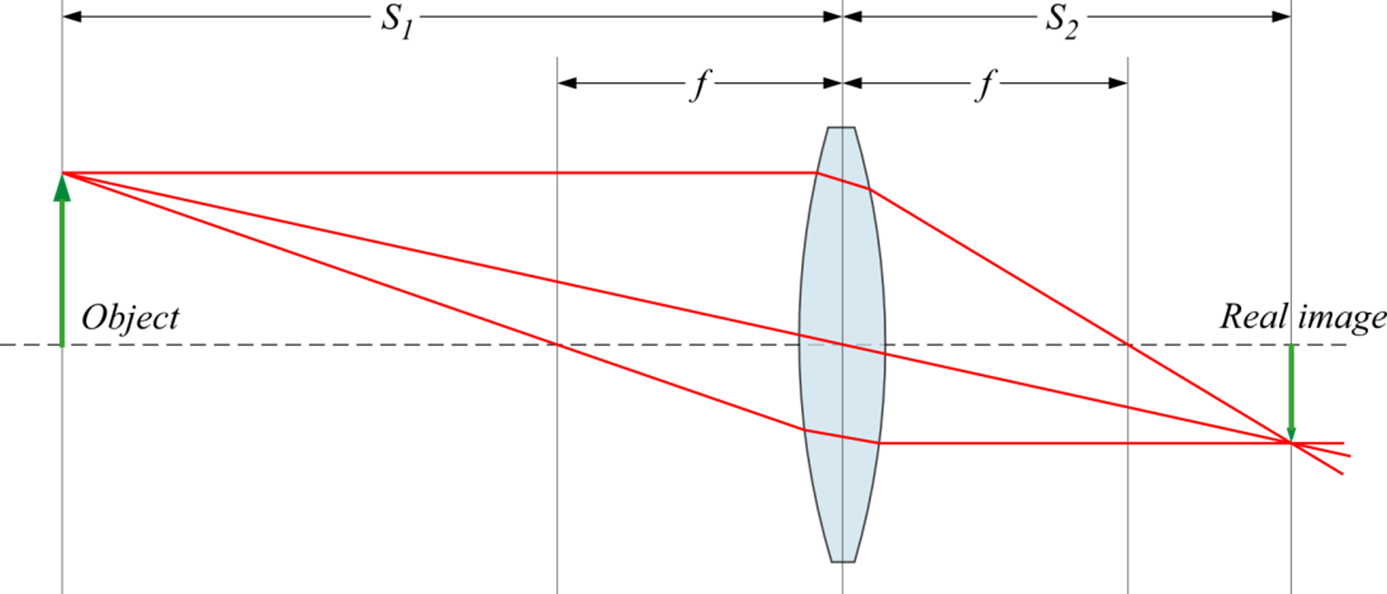
One of the simplest ways to model the effect of a lens is the thin lens equation, which is based on a ray model of light (see Figure 3).

\[ \frac{1}{S_1}+\frac{1}{S_2}=\frac{1}{f}\]

  1. Redraw Figure 3 to show how it would change when the light is modeled as a Gaussian beam, rather than rays. In particular, where should the beam waists occur? What determines the relative width of the beam waist?
  2. Experimentally test the accuracy of the thin lens equation for the imaging of Gaussian beams. Your data from the previous question can probably be used. Is the agreement within the estimated uncertainties?
  3. Systematic errors: Under what conditions should the thin lens equation be most valid? How do these conditions compare to conditions of your actual measurements? Can you get better agreement?
Figure 3: Diagram showing the focusing of light by a thin lens in the ray approximation. The diagram identifies the quantities in the thin lens equation: image distance, object distance, and focal length.

5 Appendix: LabVIEW Automation Guide

5.1 Setting up the motor

If you are using your own laptop, you will likely need to download additional device drivers for LabVIEW (the software should already be installed on the lab computers). You should download the APT software here in order to get the MGMotor library used below (you should install the 32-bit software for 64-bit Windows if you have the 32-bit version of LabVIEW installed, and the 64-bit software for 64-bit Windows if you have the 64-bit version of LabVIEW installed). Once you have done this, follow the next steps:

  1. Start with LabVIEW closed on your computer and no cords connected to the motor cube.
  2. Connect the USB to the KST101 controller cube, THEN turn on the power. If you receive a device driver loading error, you’ll likely need to disable the Memory Integrity Core Isolation device protection feature in Windows Security. If you get this error on a lab computer, please find a technical staff member for assistance.
  3. Open APT Config on the computer. Your motor should be seen by the software. Click the motor drop down menu and select your motor. Now, in the drop down menu for Stage, find ZST225(B) and select it. With these options in place, select the Add/Change Stage Association button.
  4. Close APT Config.

This should connect the motor correctly, but to verify, open APT User. This will open a LabVIEW VI with a motor control on the front panel. This motor control should have your serial number in the top right corner and should also have “STAGE: ZST225(B)”. Clicking the arrow pointing up and arrow pointing down should move the motor in either direction. If none of this is seen when you open APT User, the motor was not set up correctly and you should disconnect the USB and power supply from the motor and start again at Step 1.

5.2 LabVIEW VI implementation

To understand how to automate the data taking process using LabVIEW, consider what you do while taking data by hand. The process includes: moving the razor (stage), reading the position, reading the photodiode voltage, repeat. In order to automate this process, two pieces of equipment are used: the motor to move the stage and the NI-DAQ to read the voltage.

The first step in data taking is moving the razor. To automate this, we need to use the motor cube. To connect the cube to LabVIEW, follow these steps:

  1. On the front panel, place an ActiveX Container (Under the “.NET & ActiveX” tab)
  2. Right click the ActiveX Container > Insert ActiveX Object ... > MGMotor Control
  3. Right click MG17Motorin the block diagram > Create > Property for MG17MotorLib… > HWSerialNum
  4. Right click HWSerialNum > Change to Write
    1. Wire the MG17Motor reference out to the reference in of HWSerialNum. This allows us to tell the LabVIEW to look for the motor cube with your serial number (i.e. your cube).
  5. Add a Numerical Control to the front panel.
    1. Rename to HWSerialNum
    2. In the block diagram, wire it to the input of HWSerialNum. This control allows you to input your motor’s serial number easily on the front panel in case you change cubes.
  6. Right click MG17Motor in block diagram > Create > Method for MG17MotorLib… > StartCtrl
    1. Wire the reference out of HWSerialNum node to reference in of StartCtrl.
    2. At this point, our LabVIEW is basically saying “Look for a motor with this serial number (input in the front panel numerical control) and start controlling it.” Now we have to make it move.
  7. Right click MG17Motor in block diagram > Create > Method for MG17MotorLib… > SetJogStepSize
    1. This node allows us to tell the motor how much to move and it uses units of millimeters.
    2. Wire the reference out of StartCtrl to reference in of SetJogStepSize.
  8. Add a Numerical Control on front panel
    1. Rename it Set Jog Step Size (mm)
    2. In the block diagram, wire this control to fStepSize input of SetJogStepSize
    3. Connect reference out of StartCtrl to reference in of SetJogStepSize.
  9. Add a Numerical Constant of 0 in the block diagram
    1. Wire to the IChanID input of SetJogStepSize
    2. This concludes the initialization portion of the LabVIEW.
  10. Right click MG17Motor icon in block diagram > Create > Method for MG17MotorLib… > SetJogVelParams
    1. Wire the reference out of HWSerialNum to reference in of this block.
  11. Add three Numerical Controls to the front panel.
    1. Rename one to Min Velocity (mm/s) and wire it in the block diagram to the fminVel input of SetJogVelParam.
    2. Rename one to Max Velocity (mm/s) and wire it in the block diagram to the fmaxVel input of SetJogVelParam.
    3. Rename the last numerical constant Acceleration (mm/s/s) and wire it in the block diagram to the faccn input of SetJogVelParam.
    4. These control how the motor moves. They should be set to a minimum velocity of 0 mm/s, a maximum velocity of 1 mm/s, and an acceleration of 1 mm/s/s.

The next step involves the action that we want the motor to execute, as well as the data taking process:

  1. In order to separate the ‘action’ part of the LabVIEW from the ‘initialization’, first add a Flat Sequence Structure in the block diagram under the Structures tab.

    1. Drag the Flat Sequence Structure to include everything in the block diagram so far (the initialization part).
    2. Right click the Flat Sequence Structure and select Add Frame After. The second frame in this sequence loop will contain all the action of moving the motor and taking the data.

  2. The data taking process has one key feature that should be addressed at this point, the “repeat” part (Move razor, take data, repeat). In order to make our LabVIEW repeat this process:

    1. Add a While Loop (from the Structures tab) inside the second frame of the Sequence.
    2. Add a Stop button to the front panel and, in the block diagram, wire the stop button to the red stop circle in the corner of the While Loop. This loop will execute its contents repeatedly while the loop has a Boolean “true” value. Once the LabVIEW is running, pressing this stop button on the front panel will stop the While Loop from continuing.

  3. We need to put our other actions inside this While Loop. We want these actions to be performed in a sequence, so inside the While Loop, add another Flat Sequence Structure (we will refer to this loop as sequence #2).

    1. Add 3 frames to sequence #2 for a total of 4 frames.

  4. Inside the first frame of sequence #2, we want the razor to move one Jog Step.

    1. Right click MG17Motor > Create > Method for MG17MotorLib… > MoveJog and place inside 1st frame of sequence #2.
    2. Wire reference out from SetJogStep node to reference in of MoveJog.
    3. Add a Numerical Constant of 0 to the block diagram and wire it to the IChanID input.
    4. Add one Numerical Control to the front panel and rename it Jog Direction.
    5. Wire it to the IJogDir input and enter its value as either 1 or 2 (the values correspond to extending or retracting).

  5. The next step in the data taking process to wait some amount of time to ensure we do not read the photodiode voltage while the razor is moving.

    1. Add the Wait function (under the Timing tab) to the 2nd frame of sequence #2.
    2. Add a Numerical Control to the front panel, rename it Wait (ms).
    3. Wire this control to the Wait function. This allows you to change the wait time from the front panel.

  6. At this point we need to introduce the NI-DAQ. First, find a working DAQ. Plug it into the computer via the USB. Wire the BNC output from the photodiode into the +/- analog inputs of the DAQ labeled AI0.

    1. In the 3rd frame of sequence #2 add Measurement I/O >: NI-DAQmx > DAQ Assist.
    2. A window should pop and you should click Acquire Signal > Analog Input > Voltage > Channels ai0.
    3. A new window should pop up for additional setting options called DAQ Assist Properties. Under Timing Settings, change the Acquisition Mode to 1 Sample (On Demand).
    4. Click OK to close the window and save your settings.

  7. In the 4th frame of sequence #2 select File I/O > Write to Measurement File

  8. A window should open for properties of this node, if it does not then right click the Write to Measurement File icon and select “Properties”.

    1. Under the Filename section, select Ask User to Choose and check the box Ask Only Once. This allows you to enter the file name when LabVIEW is run.
    2. Under If a file already exists select Append to file. This makes it so each data point is added to the same file, instead of overwriting or deleting old data points.
    3. The file format should be left as text format because it’s easiest to upload into Mathematica.
    4. Under the header option, select No Headers. At this point all the settings should be as we want so close this window.

  9. Now we need to feed our data into this icon so it knows what to write to file. The data that we want should be in the form (position, voltage).

    1. In sequence #2 frame 4 add Express > Sig. Manip. > Merge Signals.

  10. This merged signal will output to the Write to File node and we want the position value in the upper input of Merge Signals and the voltage value in lower input.

    1. Wire the Data output from the DAQ-Assist icon in frame 3 to the lower input of the Merge Signals operator.
    2. Add a Numerical Indicator on the front panel and rename it Voltage (V) and wire the data output of the DAQ-Assist to it in the 3rd frame of sequence #2 in the block diagram. This provides a real-time check of the photodiode voltage from the front panel.

  11. We want to know the position of the stage. Right click MG17Motor > Create > Method for MG17MotorLib… > GetPosition and place the icon in the 3rd frame of sequence #2.

    1. Wire the reference out from MoveJog to the reference in of GetPosition.
    2. Wire a Numerical Constant to the IChanID input and enter its value as 0.
    3. Right-click on pfPosition and select Create > Indicator to give us a real-time indicator of the position.
    4. Right-click the new indicator and select Create > Local variable.
    5. Right-click on the new local variable and select Change to read and wire it to the input of pfPosition.
    6. Wire the output of pfPosition to the upper input of the Merge Signals operator.

  12. Now the data is in the form (position, voltage) and the merged signal should be wired into the Signals input of the Write to File node.

And with that, the LabVIEW setup is complete!

At this point, take a step back and take a look at the big picture of the LabVIEW and how it operates. There are many different approaches to automating this specific process and there is always more than one way to approach any problem. In this case what we did was we broke up the LabVIEW into 2 major parts; the initialization and the action. To initialize, we said “look for a motor with this serial number, start controlling it and set its jog step size to be this size.” With that done, we move to the action part. The While Loop says “continue doing this until I press the stop button” and what we are telling it to do is; move the razer, wait for it to stop moving, read the photodiode voltage and combine it with the position measurement, and finally write the data to a file. Once it executes that process the While Loop starts it all over again.

Some tips on how to actually use the LabVIEW.

  1. Make sure the move velocity on the motor control cube is maxed out at 1mm/s. This is changed on the motor cube itself through the menu.
  2. The Jog Step Size can be very small (0.05 mm for example).
  3. To determine a good amount of time to wait, you can start with the kinematic equation: \(x = 1/2 a t^2\). For a step size of 0.05mm, this indicates a time of 316 ms. You may also need to worry about the maximum velocity if you have a large step size. In general, you probably want to add another 200 ms for safety. This will ensure that vibrations from the movement have damped out.
  4. Check where a good starting position is on the control cube display. Then, once a data set is taken you can quickly move the motor to the start position using the control wheel on the cube. You definitely want to include data before, during, and after the razor starts to block the light.

The final LabVIEW requires you to input the serial number, step size, and wait time on the front panel. With those values in place, running the LabVIEW and selecting the file save location are all that needs to be done to start the process. To stop, press the stop button and it will cut off the While Loop and end the process.

For more details on how LabVIEW and Thorlabs products interact, you can look this user guide.




© University of Colorado Boulder