PHYS 3330

Lab Skill Activity - Analyzing Data in Mathematica

Contents

1 Goals

You will be…

  1. …able to define and use functions in Mathematica.

  2. …able to scale and shift lists (arrays) of data.

  3. …able to generate and combine plots of data and functions.

  4. …able to perform least-squares fits of data.

  5. …able to create pretty looking plots.

2 A Few More Mathematica Basics

Defining functions that perform a sequence of mathematical or logical steps is a key part of every programming language. Watch the screencast on defining and using functions in Mathematica.

  1. Define a function in Mathematica that represents \(f(x) = sin(x)/x\)
  2. Explain the difference between how Mathematica interprets the following two expressions:
    1. y = x^3
    2. y[x] := x^3

A “List” in Mathematica is the equivalent of an “array” in most other programming languages (like C, Python, MATLAB). This exercise requires you to create a list and perform the basic list manipulations like shifting and scaling all list values by a constant. You may need to consult the Mathematica help documentation.

  1. Create a list named sinTable using the Table function to evaluate the expression Sin[x] at 100 points between \(0\) and \(4\pi\).
  2. Increase all values of the list sinTable by a constant (e.g., 1).
  3. Multiply all the values of the list sinTable by a constant value (e.g., 10).

3 Creating Plots of Data and Function Together

In Mathematica Plot is used for plotting functions and ListPlot is used for plotting data. If we want to combine a plot of a theoretical prediction or a best fit curve with our data we need to combine these two different kinds of plots. The key method is Mathematica’s Show function.

Watch the screencast on combining plots of data and functions.

  1. Write down a mathematical expression for the predicted output signal of a waveform generator for either the square wave, saw tooth wave, or triangle wave. You can write a formal math expression or use the builtin Mathematica functions for Sin, SquareWave, SawtoothWave, and TriangleWave (consult Mathematica’s help for using these appropriately).
  2. Make a plot of your prediction using the expression you created above.
  3. Scale your sinTable function from Sections 2.3-5 to the same frequency, amplitude, and offset as the expression you created in 3.1. Combine the plot of your oscilloscope data with your prediction. Do they match up exactly? If not, did you make a mistake, or is there a good reason for the difference?

4 Fitting Data

Scientists often need to perform fits to their data. This could be because they know the functional form the data should follow and use a fit to determine one or more parameters in the function. Or because they don’t know the functional form and try various functions to see which one best fits the data. After completing this activity, you will be able to use the LinearModelFit and NonlinearModelFit functions for doing least squares fitting of data. You will demonstrate your proficiency by fitting an exponential decay. The data are the number of counts detected as a function of time for cosmic ray muon decays. The data were taken in a previous semester as part of the muon lifetime lab. The decay time you estimate from the least-squares fit is the lifetime of the muon. The muon data is available here.

Watch the screencast on fitting data in Mathematica.

  1. Write down a mathematical expression for the function you will use to fit your data.
  2. How many free parameters do you need? Give a brief explanation in words, or with a graph to explain what they mean.
  3. How do you relate your fit parameters to the muon lifetime \(\tau_{muon}\)?
  4. Is the fit function linear or nonlinear?
  5. Fit the data and obtain \(\tau_{muon}\).
  6. Make a combined plot of the data and fit.

5 Making Classy Plots in Mathematica

The default plot style in Mathematica does not look very good for presentation quality graphics. This screencast give some options for changing the plot style. Figure 1 shows an example of the plot style changes you will be able to implement after watching the screencast. The screencast also demonstrates the use of the SetOptions function which allows you to set the default plot options.

Watch the screencast on changing the plot style.

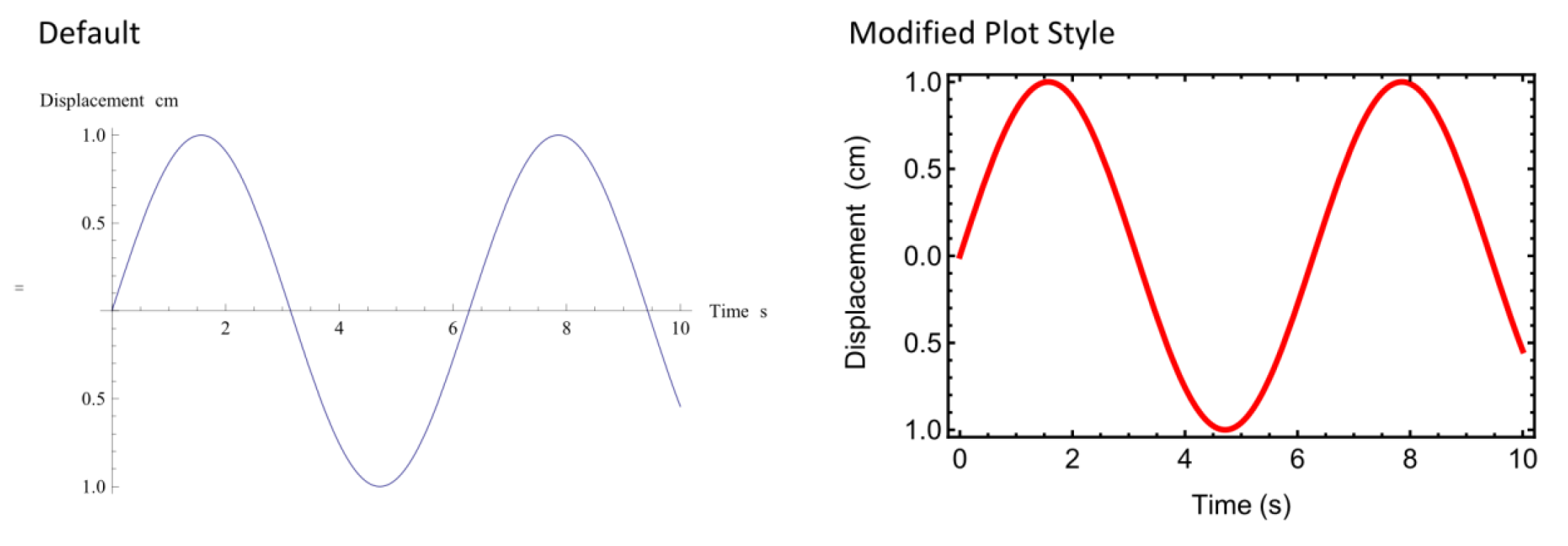
Figure 1: Plot of sin(t) for t between 0 and 10. Modifying the plot options can improve the viewing of the plot within Mathematica and for printing. Notice that the default axes and sine curve are very thin when printed.

Default

Plot[Sin[x], {x, 0, 10}, 
    AxesLabel -> {"Time (s)", "Displacement (cm)"}]

Modified

Plot[Sin[x], {x, 0, 10},
    Frame -> True,
    Axes -> False,
    LabelStyle -> {FontFamily -> "Arial", FontSize -> 13},
    FrameLabel -> {"Time (s)", "Displacement (cm)"},
    FrameStyle -> Thickness[0.005],
    PlotStyle -> {Red, Thickness[0.01]}]
  1. Modify any one of the plots produced earlier in this activity and make it “classier”.



© University of Colorado Boulder